Разработка и выбор систем координат для Toril GIS связаны с уникальными задачами картографирования фэнтезийных миров. Этот процесс подчеркивает важность точности и настройки для обеспечения точной интеграции разнообразных геопространственных данных.

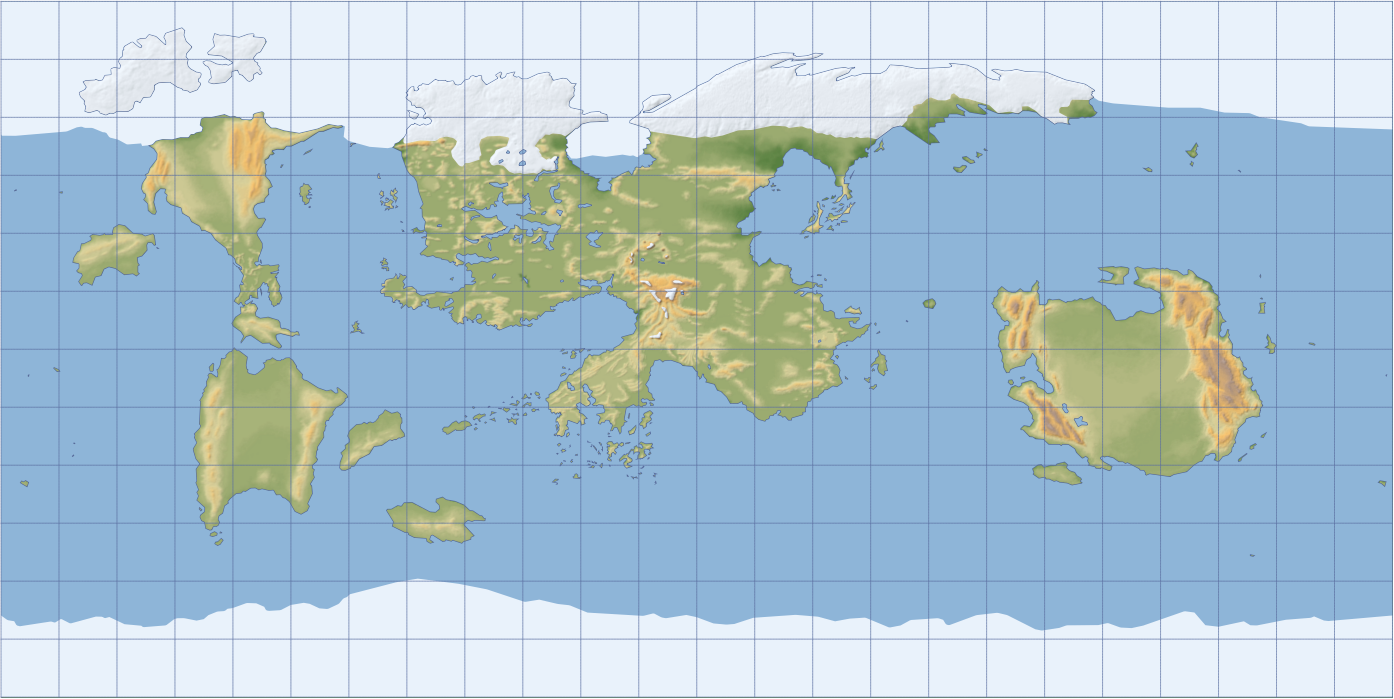
Забытые Королевства (сокращённо FR, или Forgotten Realms) — это популярный игровой сеттинг для Dungeons & Dragons (D&D), действие которого разворачивается на вымышленной планете Торил. Чтобы приступить к созданию карт для Торила, надо определиться с системой координат (СК). Если взять официально опубликованные карты и атласы FR, такие как Forgotten Realms Atlas (1990) и Forgotten Realms Interactive Atlas (1999), то там вы не найдёте указаний о конкретно используемых СК. Однако, изучив карты внимательно, можно сделать обоснованное предположение, что большинство карт созданы в равнопромежуточной проекции, где сетка параллелей и меридианов формирует идеальные квадраты с востока на запад и от полюса до полюса. Это просто и удобно, потому что географические координаты можно прямо наносить на карту.

Географическая система координат

ГСК основывается на сфере или сплюснутой сфере (эллипсоиде), а местоположения задаются угловыми измерениями, выраженными в градусах, отображаемые потом на плоскости в равнопромежуточной проекции. Размеры эллипсоида Торила уже известны: он определяется экваториальной осью \(a\) 6410 км (3983 мили) и полярной осью \(b\) 6370 км (3958 мили). Если перевести это на технический язык ГИС, то описание ГСК Торила в формате WKT-CRS будет следующим:

GEOGCRS["Toril GCS",
    DATUM["Toril",
        ELLIPSOID["Toril",6410000,160.25,
            LENGTHUNIT["metre",1]]],
    PRIMEM["FRIA",0,
        ANGLEUNIT["degree",0.0174532925199433]],
    CS[ellipsoidal,2],
        AXIS["latitude (Lat)",north,
            ORDER[1],
            ANGLEUNIT["degree",0.0174532925199433]],
        AXIS["longitude (Lon)",east,
            ORDER[2],
            ANGLEUNIT["degree",0.0174532925199433]],
    USAGE[
        SCOPE["Web mapping and visualisation of Toril."],
        AREA["World."],
        BBOX[-90,-180,90,180]]]

Этот код можно использовать в диалоговом окне пользовательской СК в QGIS. Обратите внимание, что для определения эллипсоида в WKT-CRS вместо полярной оси \(b\) используется обратная величина коэффициента сжатия эллипсоида Торила, которая рассчитывается как \(\frac{1}{f} = \frac{a}{(a-b)}\) и равна 160,25.

Если мы возьмём существующие карты FR и c помощью QGIS “привяжем” их в только что определённой ГСК, то увидим, что нулевой меридиан (сокращённо PM, или Prime Meridian; находится посередине изображения) пройдёт рядом с городом Чопхон (Chophon) в горной стране Табот в Центральном Кара-Туре. Он не был задан так специально, как в случае с Гринвичским меридианом на Земле, а находится там просто по факту. Для устранения неоднозначности, я присвоил этому случайному меридиану название FRIA PM (по имени источника карт: Forgotten Realms Interactive Atlas), чтобы не путать его с ещё одним нулевым меридианом — MD PM (по имени древнего города Myth Drannor). Мит-драннорский меридиан был упомянут Эдом Гринвудом, создателем сеттинга FR, как возможный аналог нашего гринвичского. Однако в ГСК с MD PM, 180-меридиан “режет” пополам восточный континент Оссэ.

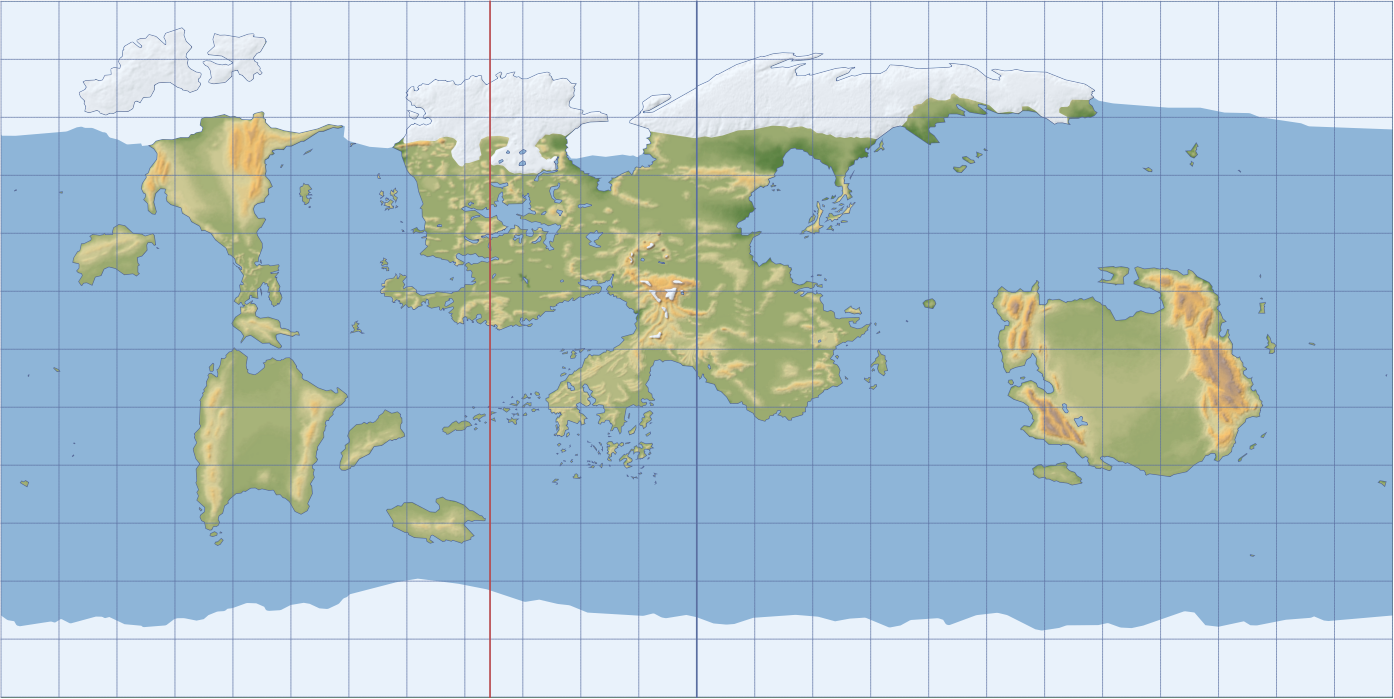Карта Торила в ГСК (равнопромежуточная проекция), отцентрированная по FRIA-меридиану (синяя линия), как в исходном материале. Красная линия показывает MD-меридиан в соответствии с лором FR.

Я бы и хотел использовать MD PM в качестве основы, чтобы соответствовать лору, однако это сильно усложнит жизнь, так как все исходные карты придётся обрабатывать прежде чем привязывать их в ГИС: придётся отрезать восточную часть изображения и перемещать её влево. В итоге я решил сделать так: для простоты все данные в Toril GIS будут геопривязаны относительно FRIA PM в любых ГСК, однако когда необходимо измерить координаты относительно MD PM, то достаточно будет пересчитать только долготу:

\[\lambda_{\text{MD}} = \lambda_{\text{FRIA}} + 53,48°\] \[\lambda_{\text{MD}} = \begin{cases} \lambda_{\text{MD}} — 360° & \text{если } \lambda_{\text{MD}} > 180° \\ \lambda_{\text{MD}} + 360° & \text{если } \lambda_{\text{MD}} < -180° \\ \lambda_{\text{MD}} & \text{в противном случае} \end{cases}\]

Вот, координаты некоторых локаций в СК Toril GCS относительно FRIA и MD нулевых меридианов:

Локация Континент Широта (FRIA и MD) Долгота FRIA Долгота MD
Мит Драннор (Myth Drannor) Фаэрун +41.41° -53.48° 0°
Глубоководье (Waterdeep) Фаэрун +45.20° -73.63° -20.15°
Конигейм (Konigheim) между Фаэруном и Кара-Туром +9.89° -14.90° +38.58°
Тукан (Tukan) Мазтика +15.23° -115.98° -62.5°

Как видите, координаты — это дело относительное.

Системы координат проекции

Я ещё не видел мир Забытых Королевств в СК отличных от ГСК. Как отправной пункт ГСК хороша, однако для красивой визуализции надо поэкспериментировать с системами координат проекции (СКП), которые основываются на ГСК и проекции карты. Проекция карты содержит математические вычисления для конверации угловых координат в декартовы координаты на плоскости. Ниже я привожу список таких СКП, которые я посчитал приемлимыми для Toril GIS.

Проекция Мольвейде

Равновеликая псевдоцилиндрическая картографическая проекция.

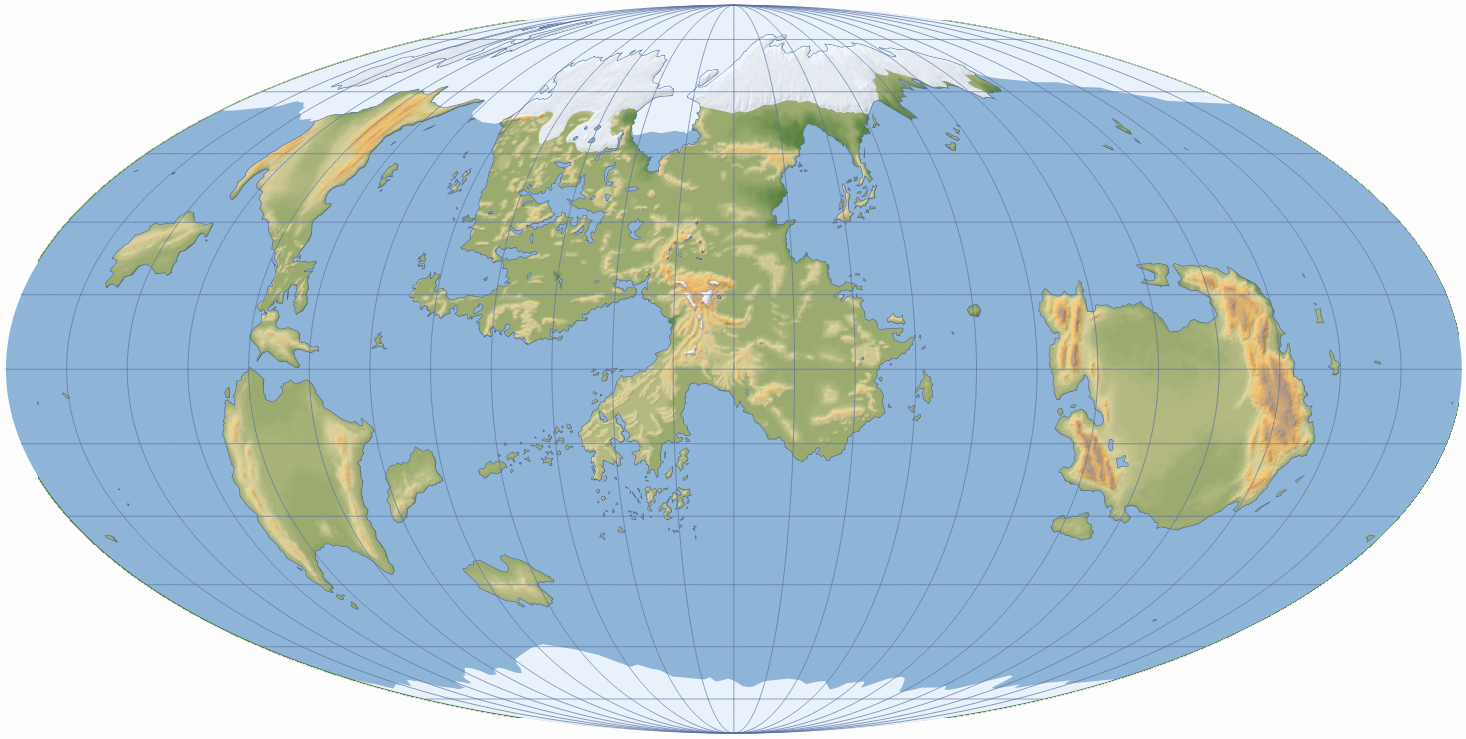Карта Торила в проекции Мольвейде, отцентрированная по FRIA-меридиану.

Проекция Бермана

Цилиндрическая равновеликая картографическая проекция. Сильно сжимает полярные области. Но ведь в них и так ничего нет, верно?

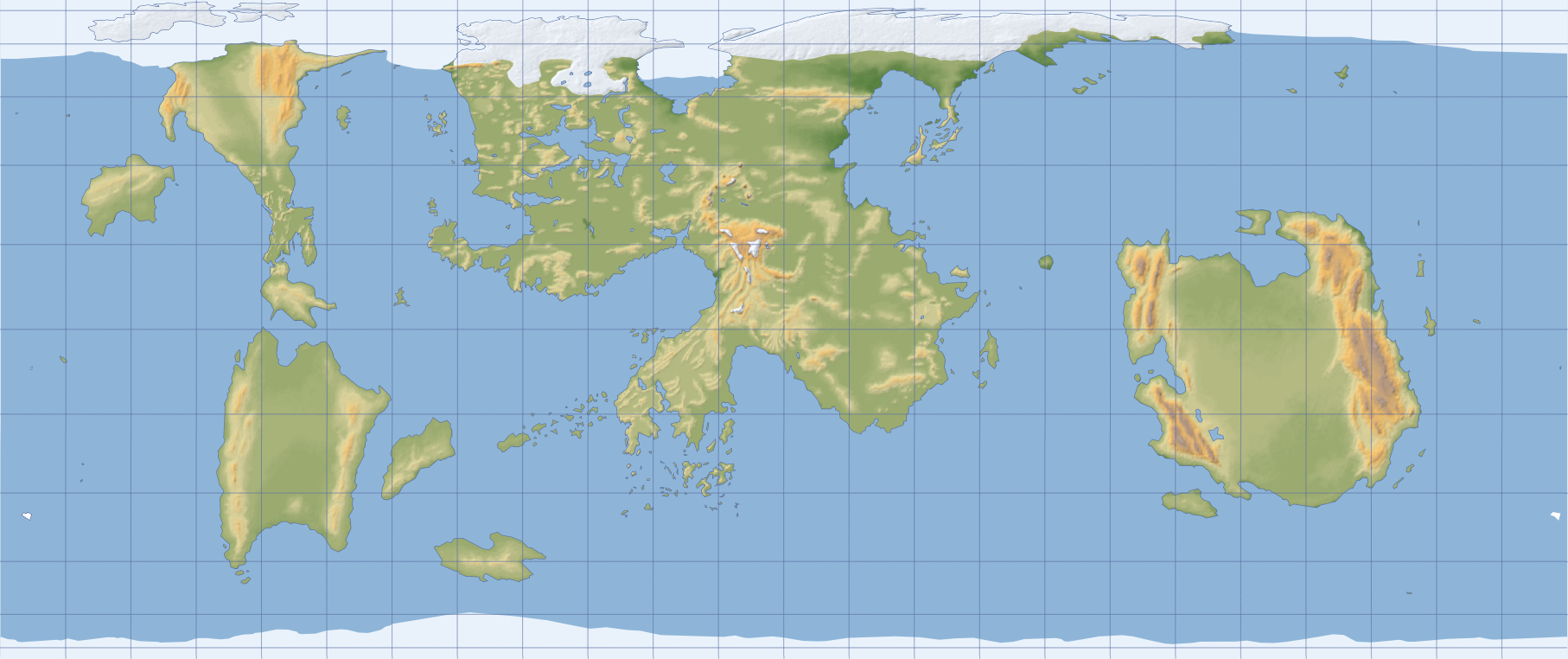Карта Торила в проекции Бермана, отцентрированная по FRIA-меридиану.

Ортографическая проекция

Она изображает полушарие Торила, как оно видно из космоса, сильно искажая области вблизи краев. Это даёт наилучшее отображение всего полушария.

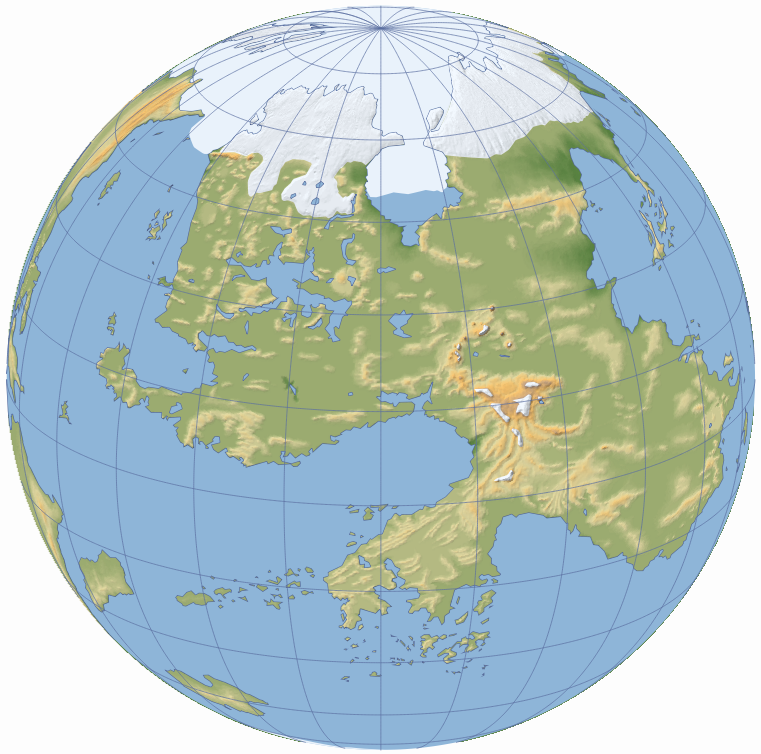Toril Planet in the orthographic projection Карта Торила в варианте ортографической проекции, центрированная на Фаэруне.

Проекция Меркатора

На самом деле эта проекция бесполезна для Toril GIS и я не буду её использовать, так как она сильно растягивает полярные области. Я поместил её здесь, чтобы дать вам больше представления о проекциях.

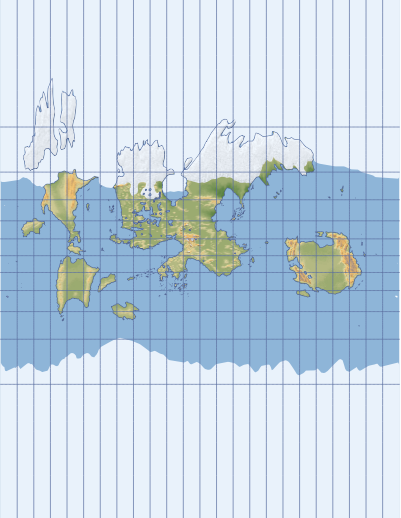Карта Торила в проекции Меркатора, отцентрированная по FRIA-меридиану.

Файлы WKT-CRS с описанием всех упомянутых СК можно скачать из репозитория Toril GIS.